ボリンジャーバンドという名前を聞いたことがありますか?
ボリンジャーバンドはトレンドの強さや
トレンドやボラティリティを分析するためのテクニカル指標で
相場の変動幅に応じて上下に動くバンドで表され、相場の上限や下限を知ることができます。
この記事では
毎日、日経平均やGAFAMの株価チャートとボリンジャーバンドをPythonで出力して
自動でツイッターで投稿している僕が
ボリンジャーバンドについて基礎から応用まで詳しく解説します。
初心者の方でも理解しやすいように、Pythonを使った実装方法も紹介します。
ボリンジャーバンドとは?

ボリンジャーバンドは株価や為替などの価格変動の標準偏差を利用して、
価格がどの程度変動しやすいかを示す指標です。
移動平均線を基準に上下に標準偏差の値を足し引きしたラインで構成されます。
トレンドの方向性やその強さ、価格の変動幅やレンジの幅、高値や安値の水準など、
さまざまな市場情報が視覚的に分かります。
移動平均は過去の記事を参考にして下さい。
-

-
テクニカル分析に役立つ!Pythonで移動平均計算と実装方法
時系列データの分析には移動平均が不可欠です。 また、移動平均には複数の種類があり、それぞれに特徴があるのでどれを使うかはデータの性質によって異なります。 Pythonを使えば簡単に移動平均を計算し、デ ...
続きを見る
さらに、ボリンジャーバンドは、価格が上限や下限に達した時に反発する可能性が高いので、
今後の相場の展開を予想することができます。
ボリンジャーバンドの基本的な使い方は、以下の通りです。
・トレンドの方向性や範囲を判断する
・高値・安値の水準を把握する
ボリンジャーバンドの計算式

ボリンジャーバンドの計算式は以下の通りです。
・中央線(単純移動平均)=n日間の終値の平均
・上限バンド=中央線+k×n日間の標準偏差
・下限バンド=中央線-k×n日間の標準偏差
※ここでnは期間、kは標準偏差の倍率を表します。
ボリンジャーバンドの開発者であるジョン・A・ボリンジャー( John A. Bollinger)さんは
推奨期間を20日間としています。
単純移動平均(SMA)は一定期間の価格の平均値を計算することで、
トレンドを把握する指標です。以下の記事を参考にして下さい。
-

-
テクニカル分析に役立つ!Pythonで移動平均計算と実装方法
時系列データの分析には移動平均が不可欠です。 また、移動平均には複数の種類があり、それぞれに特徴があるのでどれを使うかはデータの性質によって異なります。 Pythonを使えば簡単に移動平均を計算し、デ ...
続きを見る
標準偏差の計算方法
標準偏差はデータの散らばり具合を表す指標です。
標準偏差が小さいほどデータが集中し、大きいほど散らばっていることを示します。
数式は以下の通りです。
※σ:標準偏差
n:データを取得する期間
\(x_{i}\):各データの値
\(\overline{x}\):n日間のデータの平均
正規分布とは?
正規分布は統計学でよく用いられる確率分布の一つで、
平均値を中心とした対称な形をしています。
自然界に存在する多くの現象やデータが正規分布に従うとされ、
統計学の基本として広く用いられています。
正規分布は、以下のような特徴を持ちます。
平均値(期待値)を中心に左右対称の形をしている。
データのばらつきを表す標準偏差によって形が変わり、
標準偏差が小さいとピークが高く、標準偏差が大きいとピークが低くなります。
平均値から標準偏差の1倍、2倍、3倍などの範囲を取ると、
それぞれ約68.3%、95.4%、99.7%以内にデータが含まれることが言えます。
下の図を参考にして下さい。
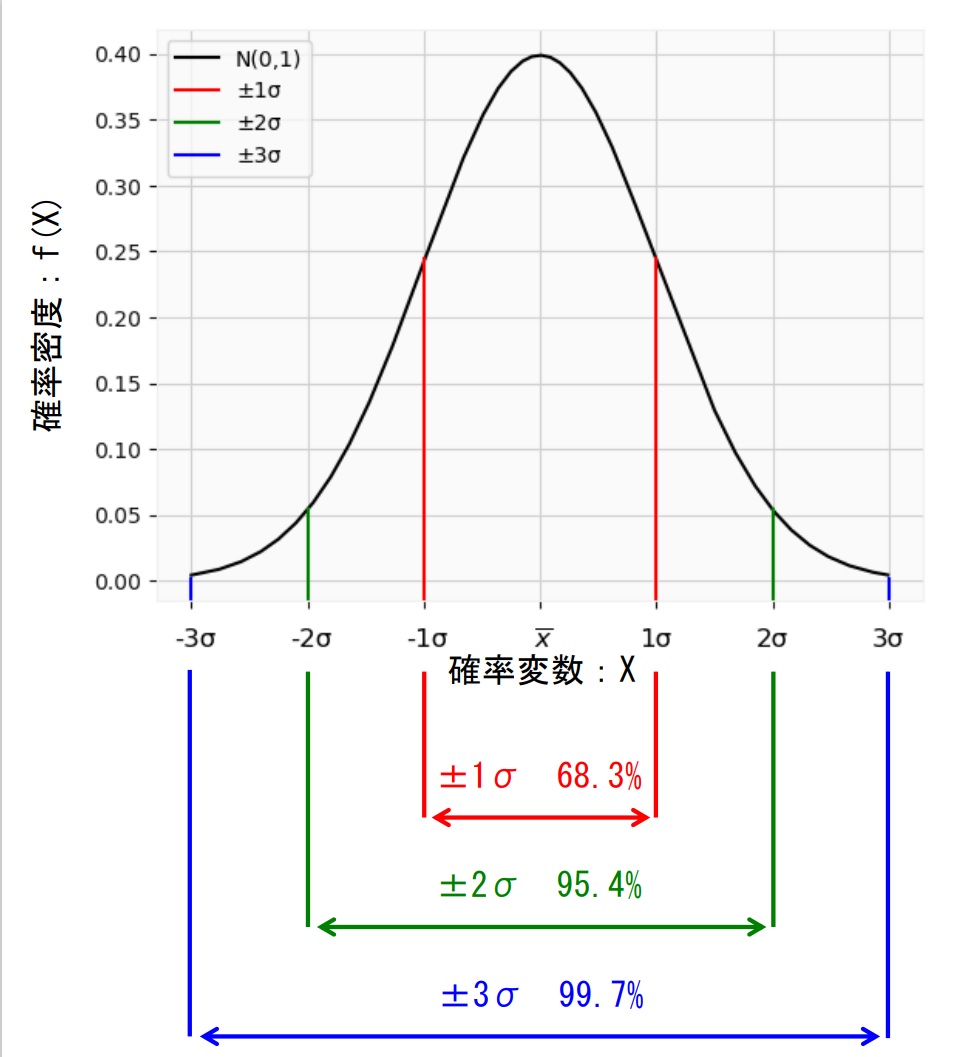
例えば身長が正規分布に従う時、平均値が170cmで標準偏差が5cmとすると、
身長が165cmから175cmの範囲にある人が約68.3%、
160cmから180cmの範囲にある人が約95.4%、
155cmから185cmの範囲にある人が約99.7%になることが予想されます。
ボリンジャーバンドの使い方

具体的なボリンジャーバンドの使い方について解説します。
ボリンジャーバンドの使い方
- トレンドの方向性を確認する
- エントリーポイントを見つける
- 利益を確定する目安にする
- 損切の目安にする
トレンドの方向性を確認する
ボリンジャーバンドは20日移動平均線を中心に、
上下に1~3倍の標準偏差を足し引きして描かれます。
このバンドが広がるほど相場のボラティリティが高まっていることを示し、
バンドが狭まるほど、相場のボラティリティが低下していることを示します。
バンドの上下位置も重要です。
バンドが上昇している場合は上昇トレンドで、
バンドが下降している場合は、下降トレンドがあると考えることができます。
エントリーポイントを見つける
ボリンジャーバンドは相場の変化点を示すことができます。
上部バンドを超えた場合は相場が買われ過ぎ、下部バンドを下回った場合は
相場が売られ過ぎと考えることができます。
利益を確定する目安にする
ボリンジャーバンドを使用して利益を確定することもできます。
トレンドが反転する前に利益を確定することができます。
たとえば、上部バンドに到達した場合には利益を確定するなどが考えられます。
損切の目安にする
逆にボリンジャーバンドを使用して損失を制限することもできます。
下部バンドを下回った場合には、損切りして損失を最小限に抑えることも考えられます。
Pythonでボリンジャーバンドの実装方法

コード全体は以下のようになります。
import mplfinance as mpf
import datetime
import pandas_datareader.data as pdr
import yfinance as yf
yf.pdr_override()
# 期間
start="2022-10-01"
end = datetime.datetime.today()
# 銘柄(トヨタ自動車)
ticker="7203" + ".T"
# データ取得
df=pdr.get_data_yahoo(ticker,start,end)
df.sort_index(ascending=True,inplace=True)
# ボリンジャーバンドを計算
r = df['Close'].rolling(20)
df['upper3'] = r.mean() + 3 * r.std()
df['upper2'] = r.mean() + 2 * r.std()
df['upper1'] = r.mean() + 1 * r.std()
df['mean'] = r.mean()
df['lower1'] = r.mean() - 1 * r.std()
df['lower2'] = r.mean() - 2 * r.std()
df['lower3'] = r.mean() - 3 * r.std()
df_upper3_max=df['upper3'].max()+10
df_lower3_min=df['lower3'].min()-10
apd_oscilator = [
mpf.make_addplot(df[['upper3', 'upper2', 'upper1','mean', 'lower1', 'lower2', 'lower3']],width=1)
]
# チャート描写
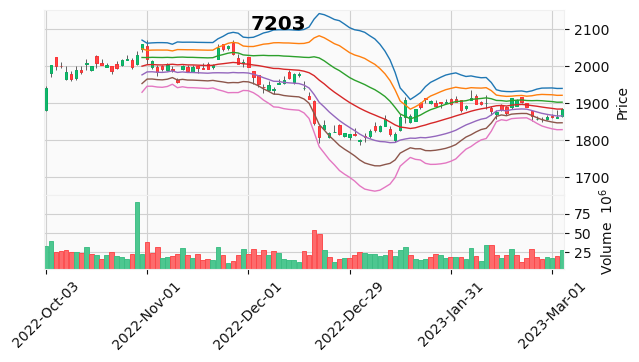
mpf.plot(df, type='candle',style='yahoo',volume=True,tight_layout=True,title=str(7203),
addplot=apd_oscilator,figsize=(6,3),ylim=(df_lower3_min,df_upper3_max))実行するとしたの画像が出力されると思います。
# ボリンジャーバンドを計算
r = df['Close'].rolling(20)
df['upper3'] = r.mean() + 3 * r.std()
df['upper2'] = r.mean() + 2 * r.std()
df['upper1'] = r.mean() + 1 * r.std()
df['mean'] = r.mean()
df['lower1'] = r.mean() - 1 * r.std()
df['lower2'] = r.mean() - 2 * r.std()
df['lower3'] = r.mean() - 3 * r.std()
df_upper3_max=df['upper3'].max()+10
df_lower3_min=df['lower3'].min()-10 r = df['Close'].rolling(20).mean()は終値の移動平均を計算しています。
詳しくは下の記事を参考にして下さい。
-

-
テクニカル分析に役立つ!Pythonで移動平均計算と実装方法
時系列データの分析には移動平均が不可欠です。 また、移動平均には複数の種類があり、それぞれに特徴があるのでどれを使うかはデータの性質によって異なります。 Pythonを使えば簡単に移動平均を計算し、デ ...
続きを見る
3 * r.std()では20日分のデータから3σを計算しています。
ローソク足とボリンジャーバンドをそのままプロットすると、見切れる場合があるので
+3σの最大値と-3σの最小値を取得して、y軸のプロット領域を設定するために使います。
以下がそのプログラムです。df_upper3_max=df['upper3'].max()+10df_lower3_min=df['lower3'].min()-10
mpf.plot(df, type='candle',style='yahoo',volume=True,tight_layout=True,title=str(7203),addplot=apd_oscilator,figsize=(6,3),ylim=(df_lower3_min,df_upper3_max))
のylimは先程取得した+3σの最大値と-3σの最小値の範囲内でグラフを表示します。
ボリンジャーバンドだけで使用するだけではなく、
他のテクニカル指標や経済指標と組み合わせて使用することで、
より正確な分析が可能になります。
おすすめのテクニカル分析とPython関連の書籍も紹介しておきます。
今回は以上です。









