時系列データの分析には移動平均が不可欠です。
また、移動平均には複数の種類があり、それぞれに特徴があるので
どれを使うかはデータの性質によって異なります。
Pythonを使えば簡単に移動平均を計算し、データを分析することができます。
本記事では、Pythonでの移動平均の計算方法、実装方法ついて紹介します。
移動平均を使ってトレンド分析のために、ぜひ本記事を参考にしてみてください。
毎日、日経平均やGAFAMの株価チャートと移動平均線をPythonで出力して
自動でツイッターに投稿している僕が以下の内容で解説していきます。
「移動平均」とは何か?

移動平均とは、ある時点から過去の一定期間分のデータの平均を取ることで、
全体のトレンドを把握することができます。
移動平均は、株価や為替レートの予測に利用されることが多く、
製造業や在庫管理においても需要のトレンドを把握するために使用されることがあります。
しかし、移動平均にはいくつかの欠点もあります。
例えば、期間が短すぎると短期的な変動に左右されやすく、
期間が長いと遅れが生じてしまうことがあります。
また、移動平均を用いた予測は、必ずしも正確なものではないので
移動平均を利用する時は、その限界や欠点も考慮する必要があります。
移動平均を正しく利用するには、期間の設定や欠点について理解することが重要です。
3種類の移動平均

以下のように移動平均は3種類あるので、順番に説明していきます。
3種類の移動平均
- 単純移動平均(Simple Moving Average)とは?
- 加重移動平均(Weighted Moving Average)とは?
- 指数平滑移動平均(Exponential Moving Average)とは?
単純移動平均(Simple Moving Average)とは?
単純移動平均(SMA)とはデータの一定期間における平均値を計算することで、
トレンドを把握する手法です。
指定した期間のデータを合計して期間で割ることで算出できます。
計算する期間を長く設定するとスムーズなトレンドを把握できる反面、
急激な変化すると反応が鈍くなる欠点があります。
実際に単純移動平均を計算していきたいと思います。
例えば、下の表の様に5日間の株価データがあったとして
3日間移動平均を計算します。
まずは1月3日の単純移動平均はその日を含めた直近3日間の株価を平均して
以下のように計算します。
同様に1月4日の単純移動平均は以下のように計算します。
\begin{align} 1月4日の単純移動平均=\frac{40+30+20}{3}=30 \end{align}
過去3日間の株価の平均値を計算することで、その3日間の株価の変化傾向を把握することができます。
| 日付 | 終値 | 単純移動平均 |
| 1月1日 | 10 | |
| 1月2日 | 20 | |
| 1月3日 | 30 | 20 |
| 1月4日 | 40 | 30 |
| 1月5日 | 50 | 40 |
加重移動平均(Weighted Moving Average)とは?
加重移動平均(WMA)は、過去のデータに加重を付けることによって、
新しいデータに大きな影響を与え、古いデータには小さな影響を与えることで、
滑らかな移動平均を算出する手法です。
単純移動平均(SMA)では、過去のデータと現在のデータを平等に扱いますが、加重移動平均では、データに重みを与えることで、より迅速にトレンドの変化をつかむことができます。
ただし、欠点もあり株価が激しく動く相場では、加重移動平均線ではその分の変化が顕著に出てしまうので変動の激しい相場では使いにくいです。
実際に加重移動平均を計算してみます。
当日の終値をP(t)前日の終値をP(t-1)と表記し、
n日間の加重移動平均は以下の式で計算できます。
同じく、下の表の様に5日間の株価データがあったとします。
例えば1月3日と1月4日で3日間の加重移動平均を計算すると以下のようになります。
| 日付 | 終値 | 加重移動平均 |
| 1月1日 | 10 | |
| 1月2日 | 20 | |
| 1月3日 | 30 | 23.3 |
| 1月4日 | 40 | 33.3 |
| 1月5日 | 50 | 43.3 |
指数平滑移動平均(Exponential Moving Average)とは?
指数平滑移動平均(EMA)は加重移動平均(WMA)と同様に
過去のデータに指数関数的に重みを付けることで、
より滑らかな移動平均を算出する手法のことです。
当日の指数平滑移動平均をE(t)、前日の指数平滑移動平均E(t-1)、計算期間をnとすれば
以下の式で算出できます。
しかし、計算期間の初日は指数平滑移動平均を計算できないので、
単純移動平均を使用します。
例題として、下のようなデータを用意しました。
例えば1月3日と1月4日で3日間の指数平滑移動平均を計算すると以下の通りです。
1月3日は前日の指数平滑移動平均のデータがないので単純移動平均の値、
つまり20になります。
1月4日は次のように計算します。
\begin{align} 1月4日の指数平滑移動平均=20+\frac{2}{3+1}\times(40-20)=30 \end{align}| 日付 | 終値 | 指数平滑移動平均 |
| 1月1日 | 10 | |
| 1月2日 | 20 | |
| 1月3日 | 30 | 20 |
| 1月4日 | 40 | 30 |
| 1月5日 | 50 | 40 |
Pythonで移動平均の実装方法

まずは単純移動平均の全体のコードを載せますね。
import mplfinance as mpf
import datetime
import pandas_datareader.data as pdr
import yfinance as yf
yf.pdr_override()
# 期間
start="2022-10-01"
end = datetime.datetime.today()
# 銘柄(トヨタ自動車)
ticker="7203" + ".T"
# データ取得
df=pdr.get_data_yahoo(ticker,start,end)
df.sort_index(ascending=True,inplace=True)
# 計算期間を設定
s=5 #短期
m=13 #中期
l=26 #長期
# 単純移動平均を計算
df["sma_s"] = df["Close"].rolling(s).mean()
df["sma_m"] = df["Close"].rolling(m).mean()
df["sma_l"] = df["Close"].rolling(l).mean()
apd_oscilator = [
mpf.make_addplot((df[['sma_s', 'sma_m', 'sma_l']]),width=1)
]
# チャート描写
mpf.plot(df, type='candle',style='yahoo',volume=True,tight_layout=True,title=str(7203),addplot=apd_oscilator,figsize=(6,3))次にコードの説明ですが、基本的なローソク足チャートのプロット方法は下の記事を参考にして下さい。
-

-
Pythonのmplfinanceでローソク足チャートを描く方法
過去記事でPythonで株価チャートを描けると紹介しました。 でも、プログラムでチャートを表示するのは難しいのでは?チャートだけでなく移動平均や出来高、トレンド系やオシレータ系といったテクニカル分析は ...
続きを見る
# 計算期間を設定
s=5 #短期
m=10 #中期
l=25 #長期
# 単純移動平均を計算
df["sma_s"] = df["Close"].rolling(s).mean()
df["sma_m"] = df["Close"].rolling(m).mean()
df["sma_l"] = df["Close"].rolling(l).mean()s、m、lで短期・中期・長期の計算期間を設定します。
※いろんな数値を試しすと発見があるかも?
df["sma_s"] = df["Close"].rolling(s).mean()は取得した終値(df["Close"])を使って.rolling(s).mean()と記載すれば短期間の単純移動平均が計算できます。
df["sma_m"]とdf["sma_l"]も同様です。
apd_oscilator = [mpf.make_addplot((df[['sma_s', 'sma_m', 'sma_l']]),width=1)]は計算した単純移動平均をグラフに追記するために記述しています。
具体的に後で出てくるmpf.plot(df,type='candle',style='yahoo',volume=True,tight_layout=True,title=str(7203),addplot=apd_oscilator,figsize=(6,3))のaddplotでapd_oscilatorを使用します。
プログラムを実行すると下のグラフが出力されると思います。
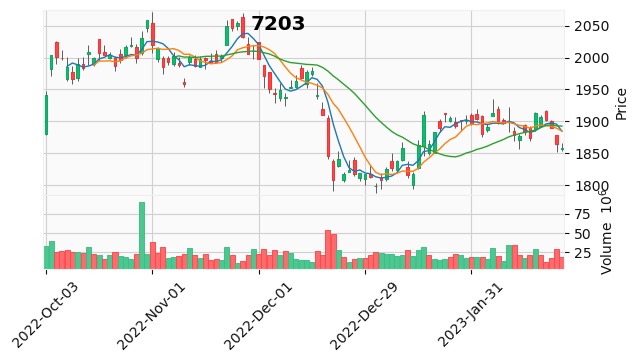
次は加重移動平均のコードです。
import mplfinance as mpf
import datetime
import pandas_datareader.data as pdr
import yfinance as yf
import numpy as np
yf.pdr_override()
# 期間
start="2022-10-01"
end = datetime.datetime.today()
# 銘柄(トヨタ自動車)
ticker="7203" + ".T"
# データ取得
df=pdr.get_data_yahoo(ticker,start,end)
df.sort_index(ascending=True,inplace=True)
# 加重移動平均
def calc_wma(prices):
weights = np.arange(len(prices)) + 1
wma = np.sum(weights * prices) / weights.sum()
return wma
# 計算期間を設定
s=5 #短期
m=10 #中期
l=25 #長期
df['wma_s'] = df["Close"].rolling(s).apply(calc_wma)
df['wma_m'] = df["Close"].rolling(m).apply(calc_wma)
df['wma_l'] = df["Close"].rolling(l).apply(calc_wma)
apd_oscilator = [
mpf.make_addplot((df[['wma_s','wma_m','wma_l']]),width=1)
]
# チャート描写
mpf.plot(df, type='candle',style='yahoo',volume=True,tight_layout=True,title=str(7203),addplot=apd_oscilator,figsize=(6,3))# 加重移動平均
def calc_wma(prices):
weights = np.arange(len(prices)) + 1
wma = np.sum(weights * prices) / weights.sum()
return wmadefで加重移動平均を計算するための関数を作っていきます。
※関数の作成方法は別の記事で紹介しようと思いますので、
今はそんなものもあるんだなと思ってください。
calc_wma(prices)という関数は後に出てくる"Close"つまり終値のデータを受け取り、
加重平均を計算します。
np.arangeはNumPyの関数で、指定された範囲内の整数を生成します。(len(prices)でデータの個数を取得します。
例えば5日間の重みを計算する時、np.arange(5)としがちですが
実行結果は[0 1 2 3 4]と出力されますが
重みとしては[1 2 3 4 5]で計算したいので+1を追記する必要があります。
np.sum(weights * prices)で取得したデータに重みを掛けています。
weights.sum()で重みを合計しています。
# 計算期間を設定
s=5 #短期
m=10 #中期
l=25 #長期
df['wma_s'] = df["Close"].rolling(s).apply(calc_wma)
df['wma_m'] = df["Close"].rolling(m).apply(calc_wma)
df['wma_l'] = df["Close"].rolling(l).apply(calc_wma)単純移動平均と同様にs、m、lで短期・中期・長期の計算期間を設定し、rolling()関数を使用して、"Close"列のデータに対して加重移動平均を計算します。
最終的にDataFrameには、短期、中期、長期の加重移動平均が追加されます。
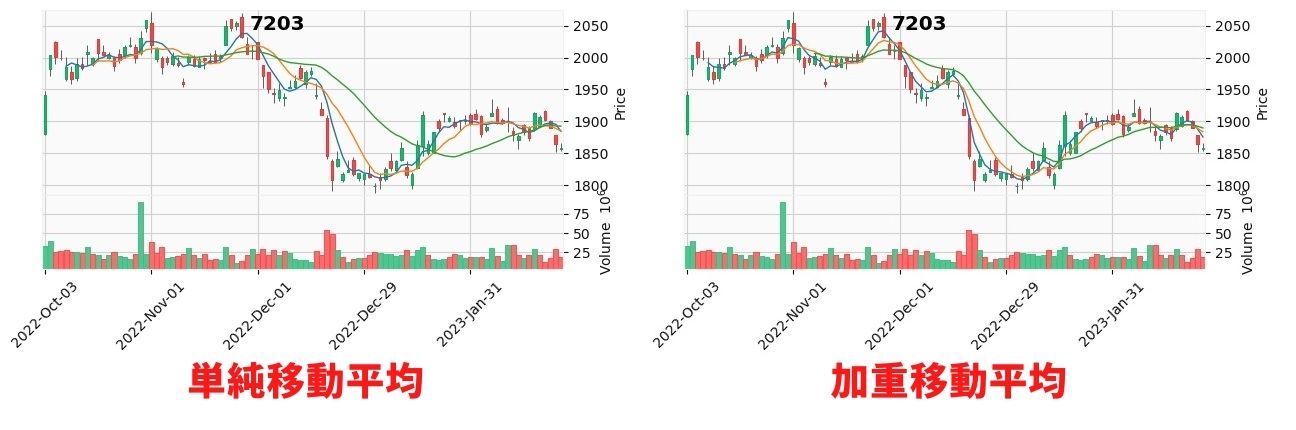
実行すると上のように加重平均がプロットされたグラフが表示されます。
単純移動平均と比較すると加重移動平均の方が滑らかにチャートに追従していることが
確認できます。
次は指数平滑移動平均のコードです。
import mplfinance as mpf
import datetime
import pandas_datareader.data as pdr
import yfinance as yf
import numpy as np
yf.pdr_override()
# 期間
start="2022-10-01"
end = datetime.datetime.today()
# 銘柄(トヨタ自動車)
ticker="7203" + ".T"
# データ取得
df=pdr.get_data_yahoo(ticker,start,end)
df.sort_index(ascending=True,inplace=True)
# 指数平滑移動平均
def calc_ema(prices, period):
ema = np.zeros(len(prices))
ema[:] = np.nan # NaN で初期化
ema[period-1] = prices[:period].mean() # 最初だけ単純移動平均
for d in range(period, len(prices)):
ema[d] = ema[d-1] + (prices[d] - ema[d-1]) / (period + 1) * 2
return ema
# 計算期間を設定
s=5 #短期
m=10 #中期
l=25 #長期
df['ema_s'] = calc_ema(df["Close"], s)
df['ema_m'] = calc_ema(df["Close"], m)
df['ema_l'] = calc_ema(df["Close"], l)
apd_oscilator = [
mpf.make_addplot((df[['ema_s','ema_m','ema_l']]),width=1)
]
# チャート描写
mpf.plot(df, type='candle',style='yahoo',volume=True,tight_layout=True,title=str(7203),addplot=apd_oscilator,figsize=(6,3))
# 指数平滑移動平均
def calc_ema(prices, period):
ema = np.zeros(len(prices))
ema[:] = np.nan # NaN で初期化
ema[period-1] = prices[:period].mean() # 最初だけ単純移動平均
for d in range(period, len(prices)):
ema[d] = ema[d-1] + (prices[d] - ema[d-1]) / (period + 1) * 2
return emadef calc_ema(prices, period)はpricesとperiodの2つの引数を持つ関数です。pricesは終値データでperiodは指数平滑移動平均(EMA)の期間を表します。
ema = np.zeros(len(prices))でpricesのデータ分の0配列を作成します。
ema[:]ではema 全ての要素を選択して、配列をNaNで初期化します。
※まだ計算されていない時は、NaNで埋めておきます。
ema[period-1] = prices[:period].mean()はemaリストのperiod-1番目の要素にpricesリストの先頭から period 個の要素の平均値を代入しています。
要は最初だけ単純移動平均を計算しています。
for d in range(period, len(prices)):ではperiodからlen(prices)つまりpricesのデータの個数までdが繰り返されます。ema[d] = ema[d-1] + (prices[d] - ema[d-1]) / (period + 1) * 2で
指数平滑移動平均(EMA)を計算しています。
実行するとしたのグラフが描写されます。
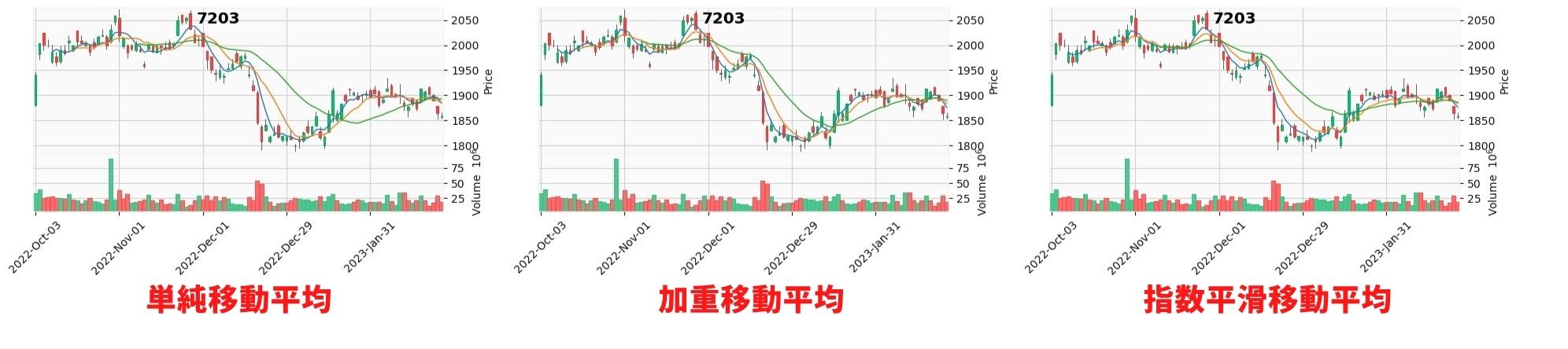
まとめ
移動平均は時系列データのトレンドを分析するための基本的な手法の一つです。
Pythonを使った移動平均の計算方法や実装方法を学べたと思います。
移動平均は、単純移動平均、加重移動平均、指数平滑移動平均の3種類があり、
Python使用することで簡単に実装することができます。
実際に移動平均を用いたデータ分析には、株価データのトレンド分析や
気温データの季節性の分析、不良品の数のトレンド分析など、
さまざまな分野で応用できるので移動平均は時系列データの分析に欠かせない方法です。
おすすめのテクニカル分析とPython関連の書籍も紹介しておきます。
今回は以上です。