『MACDって聞いたことはあるが、どう使えばいいかわからない。』
こんな悩みはありませんか?
MACDとは何か?
さらにPythonを使って基本的な使い方を初心者でもわかりやすく解説します。
毎日、日経平均やGAFAMの株価チャートをPythonで出力して
自動でツイッターで投稿している僕が解説していきます。
MACDとは?

MACDとは、Moving Average Convergence Divergenceの略で、2つの移動平均線を用いたトレンドの強弱を示すテクニカル指標です。
短期移動平均線と長期移動平均線の差を表すヒストグラムと、
その差の移動平均線(シグナル線)から構成されています。
移動平均線は下の記事を参考にして下さい。
-

-
テクニカル分析に役立つ!Pythonで移動平均計算と実装方法
時系列データの分析には移動平均が不可欠です。 また、移動平均には複数の種類があり、それぞれに特徴があるのでどれを使うかはデータの性質によって異なります。 Pythonを使えば簡単に移動平均を計算し、デ ...
続きを見る
MACDは、多くの投資家やトレーダーに利用されており、重要な指標の一つとされています。
しかし、MACDにはいくつかの問題点もあります。
例えば過去の価格変動に基づく指標であるため、
未来の価格変動を正確に予測することはできません。
また、トレンドが一度確定すると、その後の値動きに遅れが生じることがあるので、
早い段階でのエントリータイミングを求める場合には注意が必要です。
MACDの使い方

MACDは株価や為替などの価格変動を分析するためのテクニカル指標の一つで、
トレンドの転換点を予測することができます。
ここでは、MACDの使い方について解説していきますね。
MACDの使い方については以下の3つに分類されます。
MACDの使い方
- クロスオーバーの確認
- ダイバージェンス(乖離)の確認
- トレンドの確認
クロスオーバーの確認
MACDは短期移動平均線と長期移動平均線の差を表すヒストグラムと、MACDの移動平均線(シグナル線)から構成されています。
このシグナル線とのクロスオーバー(交差)が重要なサインとされています。
具体的にMACDがシグナル線を上抜けた場合には買いシグナルで、
下抜けた場合には売りシグナルと解釈されます。
ダイバージェンス(乖離)の確認
MACDは価格とのダイバージェンス(乖離)も確認できます。
例えば、価格が新高値を更新しているにも関わらず、MACDが下がり続けている場合は
売りシグナルと解釈されます。
逆に価格が新安値を更新しているのに、MACDが上がり続けている場合には、
買いシグナルと解釈できます。
トレンドの確認
トレンドの強さを確認するためにも使用されます。
MACDがプラス領域にある場合には上昇トレンド、
マイナス領域の時は下降トレンドと解釈できます。
MACDを単独で使用するのではなく、他のテクニカル指標やファンダメンタルズ分析などと組み合わせて判断することが重要です。例えば、RSIやストキャスティクスと組み合わせて使用することで、より精度の高い分析が可能になります。
MACDは過去の価格変動を基にしているので、市場環境が急激に変化する場合は
正確な予測ができないことがあります。なので常にマーケットの状況を把握してMACDの結果を慎重に検討しましょう。
MACDの算出式

MACDは移動平均線の乖離率を計算することで
価格変動を分析するテクニカル指標の一つです。
計算方法は以下の通りです。
・12日間の指数平滑移動平均線(EMA12)を求める。
・26日間の指数平滑移動平均線(EMA26)を求める。
・EMA12からEMA26を引いた値を「MACDライン」として求める。
・MACDラインに対してEMA9を適用し、「シグナルライン」として求める。
MACDの計算方法は比較的単純です。
移動平均線の期間を変更することで、トレンドの長さに合わせた分析が可能です。
また、EMAを用いることで最近の価格変動に重点を置いた分析が可能になります。
PythonでMACDの実装方法

下がコード全体となります。
import mplfinance as mpf
import datetime
import pandas_datareader.data as pdr
import yfinance as yf
yf.pdr_override()
# 期間
start="2022-10-01"
end = datetime.datetime.today()
# 銘柄(トヨタ自動車)
ticker="7203" + ".T"
# データ取得
df=pdr.get_data_yahoo(ticker,start,end)
df.sort_index(ascending=True,inplace=True)
# MACD日足
es=12
el=26
sg=9
# MACD計算
df['ema_s'] = df['Close'].ewm(span=es).mean()
df['ema_l'] = df['Close'].ewm(span=el).mean()
df['macd'] = df['ema_s'] - df['ema_l']
df['signal'] = df['macd'].ewm(span=sg).mean()
df['diff'] = df['macd'] - df['signal']
f_plus = lambda x: x if x > 0 else 0
f_minus = lambda x: x if x < 0 else 0
df['diff+'] = df['diff'].map(f_plus)
df['diff-'] = df['diff'].map(f_minus)
# サブプロット
apd_oscilator = [
mpf.make_addplot((df[['macd']]), color='r',panel=1,width=1),
mpf.make_addplot((df[['signal']]), panel=1,width=1),
mpf.make_addplot((df['diff+']), type='bar', color='r', panel=1),
mpf.make_addplot((df['diff-']), type='bar', color='b', panel=1),
]
# チャート描写
mpf.plot(df, type='candle',style='yahoo',tight_layout=True,title=str(7203),
addplot=apd_oscilator,figsize=(6,3))ここから詳細を解説してきますね。
# MACD日足
es=12
el=26
sg=9es、el、sgはそれぞれ短期・長期の指数平滑移動平均線とシグナル線の期間を
設定しています
# MACD計算
df['ema_s'] = df['Close'].ewm(span=es).mean()
df['ema_l'] = df['Close'].ewm(span=el).mean()
df['macd'] = df['ema_s'] - df['ema_l']
df['signal'] = df['macd'].ewm(span=sg).mean()
df['diff'] = df['macd'] - df['signal']
f_plus = lambda x: x if x > 0 else 0
f_minus = lambda x: x if x < 0 else 0
df['diff+'] = df['diff'].map(f_plus)
df['diff-'] = df['diff'].map(f_minus)上記のプログラムは実際にMACDを計算しています。
df['ema_s'] = df['Close'].ewm(span=es).mean()は
12日間の指数平滑移動平均線を計算します。
株価の終値df['Close']に対して、12日間の指数平滑移動平均線を求め、df['ema_s']に代入しています。
df['ema_l']は同様に26日間の指数平滑移動平均線を計算します。
df['macd'] = df['ema_s'] - df['ema_l']では短期間のEMAから長期間のEMAを引いた値を計算し、df['macd']に代入しています。
これがMACDラインに相当します。
df['signal'] = df['macd'].ewm(span=sg).mean()ではMACDに対して指定した期間(sg)のEMAを適用し、df['signal']に代入しています。
これがシグナル線に相当します。
df['diff'] = df['macd'] - df['signal']でMACDラインとシグナルラインの差分を
計算してdf['diff']に代入しています。
f_plus = lambda x: x if x > 0 else 0
f_minus = lambda x: x if x < 0 else 0
df['diff+'] = df['diff'].map(f_plus)
df['diff-'] = df['diff'].map(f_minus)最後にf_plusは正の値の場合はそのまま、負の値の場合は0にする関数で
逆にf_minusは負の値の場合はそのまま、正の値の場合は0にする関数を定義しています。
df['diff']に対して先程の関数を使って
正の時はdf['diff+']に負の場合はdf['diff-']に値を格納しています。
これでMACDとシグナル線のクロスオーバーの状態を分析する準備ができました。
# サブプロット
apd_oscilator = [
mpf.make_addplot((df[['macd']]), color='r',panel=1,width=1),
mpf.make_addplot((df[['signal']]), panel=1,width=1),
mpf.make_addplot((df['diff+']), type='bar', color='r', panel=1),
mpf.make_addplot((df['diff-']), type='bar', color='b', panel=1),
]
mpf.make_addplot((df[['macd']]), color='r',panel=1,width=1)は
MACDのプロット方法についてプログラムしています。
まずcolor='r'でMACDは赤色の線でプロットし、panel=1はローソク足の
下の個所にMACDを出力し、width=1で線幅を指定しています。
同様にmpf.make_addplot((df[['signal']]), panel=1,width=1)で
シグナル線のプロット方法を記載しています。
mpf.make_addplot((df['diff+']), type='bar', color='r', panel=1)はdf['diff+']の値をヒストグラムで表示するように記載しています。mpf.make_addplot((df['diff-']), type='bar', color='b', panel=1)も
同様です。
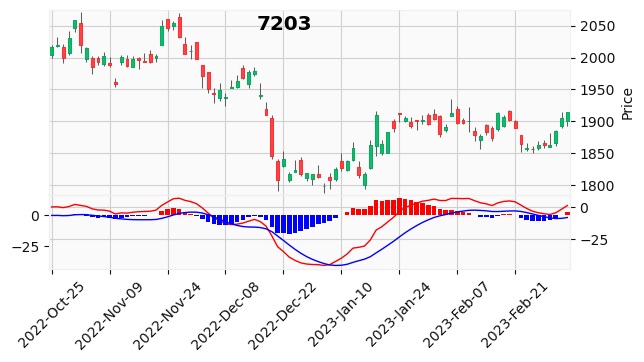
問題なく実行できれば上のような図がプロットされると思います。
以上でプログラムの解説になります。
MACDの計算は指数平滑移動平均線の計算や差分の計算が必要になりますが、
Pythonを用いれば簡単に実装することができます。
おすすめのテクニカル分析とPython関連の書籍も紹介しておきます。
今回は以上です。









